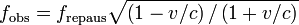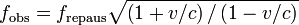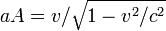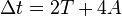Paradoxul gemenilor

În fizică, paradoxul gemenilor este un experiment imaginar din teoria relativităţii restrânse, în care o persoană care călătoreşte în spaţiu cu o navă de mare viteză se întoarce acasă şi îşi găseşte fratele geamăn identic rămas pe Pământ mai bătrân decât el. Acest rezultat pare neaşteptat, deoarece situaţia pare simetrică, întrucât fratele rămas pe Pământ poate fi considerat ca fiind şi el în mişcare în raport cu celălalt. De aceea se numeşte "paradox". Contradicţia aparentă este explicată în cadrul teoriei relativităţii.

Istoric

În celebra sa lucrare despre relativitatea restrânsă din 1905, Albert Einstein a prezis că dacă două ceasuri sunt puse împreună şi sincronizate, şi apoi unul este îndepărtat şi apoi adus înapoi, atunci ceasul care a călătorit va rămâne în urma celui care a stat pe loc. Einstein considera aceasta ca o consecinţă naturală a relativităţii restrânse, nu un paradox cum se sugera, iar în 1911, a reenunţat acest rezultat sub forma:

Dacă punem o fiinţă vie într-o cutie... poate aranja ca fiinţa, după un zbor de durată arbitrară să poată fi adusă în locul original într-o condiţie puţin modificată, în vreme ce organismele corespunzătoare rămase în poziţiile lor originale vor fi dat naştere de mult timp la noi generaţii. Pentru fiinţa în mişcare, durata călătoriei a fost doar o clipă, dacă mişcarea a fost făcută cu viteză apropiată de cea a luminii. ^[1]

În 1911, Paul Langevin a făcut acest concept mai uşor de înţeles cu al său exemplu cu gemenii, din care unul e astronaut iar celălalt trăieşte doar pe Pământ. Astronautul pleacă într-o călătorie spaţială cu o navă care merge cu viteză apropiată de cea a luminii, pe când celălalt rămâne pe Pământ. Când fratele călător se întoarce acasă, el descoperă că este mai tânăr decât fratele lui, cu alte cuvinte, dacă fraţii ar fi avut fiecare un ceas, cel al astronautului ar fi rămas în urma celui rămas asupra fratelui de pe Pământ, ceea ce înseamnă că pentru astronaut a trecut mai puţin timp decât pentru celălalt. Langevin a explicat vitezele diferite de îmbătrânire astfel: “Doar călătorul a suferit o acceleraţie care i-a schimbat direcţia vitezei”. Conform lui Langevin, acceleraţia este aici "absolută", în sensul că ea este cauza asimetriei.

Semnificaţia “Paradoxului Gemenilor” se bazează pe acest detaliu crucial al asimetriei dintre fraţi. Trebuie spus că nici Einstein nici Langevin nu au considerat aceste rezultate ca fiind literalmente paradoxale: Einstein l-a considerat doar "ciudat" iar Langevin l-a prezentat ca dovadă a mişcării absolute. Un paradox în utilizarea logică şi ştiinţifică se referă la rezultate inerent contradictorii, adică logic imposibile, şi ambii au susţinut că diferenţa de timp ilustrată de această poveste a gemenilor este un fenomen natural şi explicabil.

Exemplu

Considerăm o navă spaţială care se deplasează de pe Pământ până la cel mai apropiat sistem solar: o distanţă d = 4,45 ani lumină distanţă, cu viteza v = 0.866c (86,6% din viteza luminii, relativ la Pământ). Controlul misiunii, aflat pe Pământ, calculează astfel durata călătoriei (presupunând că imediat după plecare nava atinge viteza maximă): drumul dus-întors durează 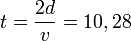ani după timpul de pe Pământ (toţi cei de pe Pământ vor fi cu 10,28 ani mai în vârstă când se întoarce nava). Trecerea timpului pe navă şi îmbătrânirea călătorilor de-a lungul acestui drum va fi încetinită cu un factor de 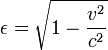, inversul factorului Lorentz. În acest caz iar călătorii vor fi îmbătrânit doar cu 0,5×10,28 = 5,14 ani la întoarcere.

Membrii echipajului calculează şi ei particularităţile călătoriei lor din punctul lor de vedere. Ei ştiu că sistemul solar îndepărtat şi Pământul se mişcă relativ la nava aflată la viteza v pe parcursul drumului. În sistemul lor în repaus, Pământul şi sistemul solar sunt εd = 0,5d = 2,23 ani lumină (Contracţia Lorentz), atât pe călătoria dus cât şi pe cea de întors. Fiecare jumătate de drum durează , iar drumul dus întors durează 2×2,57 = 5,14 ani. Calculele lor arată ca ei vor sosi acasă după 5,14 ani. Ultimul calcul al călătorilor este complet de acord cu calculele celor de pe Pământ, deşi călătoria este resimţită destul de diferit.

Dacă o pereche de gemeni se naşte pe Pământ la ora şi data plecării navei, iar unul pleacă în călătorie şi celălalt rămâne pe Pământ, ei se vor întâlni după terminarea călătoriei, şi fratele care a plecat are 5,14 ani iar cel rămas acasă are 10,28 de ani. Calculul ilustrează folosirea fenomenului de contracţie a lungimii şi a celui de dilatare temporală pentru a descrie şi calcule şi predicţii ale relativităţii restrânse.

Rezolvarea paradoxului în relativitatea restrânsă

Abordarea standard tratează paradoxul gemenilor ca o aplicaţie directă a teoriei relativităţii restrânse. Aici, Pământul şi nava nu sunt într-o relaţie simetrică: nava face o "întoarcere" în care simte forţe inerţiale, pe când Pământul nu face nicio întoarcere. Deoarece nu există nicio simetrie, nu este paradoxal faptul că un frate geamăn ajunge să fie mai tânăr ca celălalt. Cu toate acestea, tot este util să se arate că relativitatea restrânsă este consistentă, şi cum se fac calculelele din punctul de vedere al fratelui geamăn care călătoreşte.

Relativitatea restrânsă nu susţine că toţi observatorii sunt echivalenţi, ci doar aceia din sistemele de referinţă inerţiale. Dar nava spaţială accelerează la întoarcere. În contrast, fratele geamăn care rămâne acasă rămâne în sistemul inerţial pe toată durata zborului fratelui său. Asupra lui nu se aplică forţe de accelerare sau frânare.

Într-adevăr, nu sunt doar două, ci trei sisteme de referinţă inerţiale relevante: cel în care fratele rămas acasă este în repaus, cel în care fratele din navă este în repaus pe drumul de dus, şi cel în care el este în repaus pe drumul de întoarcere acasă. În timpul acceleraţiei la întoarcere, fratele care călătoreşte îşi schimbă sistemul de referinţă. În acel moment trebuie să-şi ajusteze vârsta calculată a fratelui rămas acasă.

În relativitatea restrânsă, nu există conceptul de prezent absolut. Prezentul este definit ca o mulţime de evenimente simultane din punctul de vedere al unui observator dat. Noţiunea de simultaneitate depinde de sistemul de referinţă, şi astfel trecerea de la un sistem la altul necesită o ajustare a definiţiei prezentului. Dacă ne închipuim prezentul ca pe un plan de simultaneitate (tridimensional) într-un spaţiu Minkowski, atunci trecerea de la un sistem la altul conduce la înclinarea planului.

Diagramă Minkowski pentru paradoxul gemenilor

În diagrama spaţiu-timp din dreapta, linia de univers a primului frate geamăn coincide cu axa verticală (poziţia sa este presupusă constantă în spaţiu, el deplasându-se doar în timp). La dus, al doilea frate se deplasează spre dreapta (linia neagră înclinată); la întors, se deplasează înapoi spre stânga. Liniile albastre arată planele de simultaneitate pentru fratele care călătoreşte, în timpul călătoriei dus; liniile roşii, arată planele de simultaneitate pentru întoarcere. Chiar înainte de a se întoarce, fratele din navă calculează vârsta fratelui rămas acasă măsurând intervalul de-a lungul axei verticale de la origine până la intersecţia cu cea mai de sus dreaptă albastră. Imediat după întoarcere, dacă recalculează, el va măsura intervalul de la origine la dreapta roşie cea mai de jos. Într-un fel, în timpul întoarcerii, planul de simultaneitate trece de la albastru la roşu, trecând foarte repede peste un segment larg al liniei de univers a fratelui rămas acasă. Fratele rămas acasă a îmbătrânit brusc, după calculele fratelui din navă.

Paradoxul gemenilor ilustrează o trăsătură a modelului spaţiu-timp relativist restrâns, spaţiul Minkowski. Liniile de univers ale corpurilor în mişcare inerţială sunt geodezicele din spaţiul-timp minkowskian. În geometria Minkowski liniile de univers ale corpurilor în mişcare inerţială maximizează timpul propriu scurs între două evenimente.

Asemănarea cu deplasarea Doppler relativistă

Vom vedea acum cum l-ar observa fiecare dintre fraţi pe celălalt în timpul călătoriei. Cu alte cuvinte, vom analiza cazul în care fiecare dintre fraţi are un ceas care îi indică vârsta şi ce va arăta fiecare dintre cele două ceasuri. Soluţia acestei probleme de observare se află în efectul Doppler relativist. Frecvenţa bătăilor unui ceas pe care cineva îl observă de la o sursă cu frecvenţa de repaus f_repaus este

când sursa se depărtează (reducere a frecvenţei; "deplasare spre roşu"). Când sursa se apropie, frecvenţa este mai mare ("deplasată spre albastru") şi dată de

Astfel se combină efectele dilatării temporale (reducerea frecvenţei sursei datorită mişcării ei, cu factorul ε) şi deplasarea Doppler a frecvenţei recepţionate cu un factor de (1 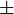v/c)^-1, care se aplică chiar şi pentru ceasuri independente de viteză (surse de lumină). Pentru cazul din exemplul de mai sus unde v / c = 0.866, frecvenţele minimă şi maximă recepţionate sunt de 3,732 şi de 0,268 de ori frecvenţa de repaus. Adică, ambii fraţi văd imaginea fratelui lor mişcându-se cu o viteză de doar 0,268 de ori viteza lor, sau invers, fiecare şi-ar măsura propria viteză de îmbătrânire ca fiind de 3,732 ori mai mare ca cea a fratelui său. Cu alte cuvinte, fiecare frate vede că pentru fiecare oră care trece pentru el, pentru fratele său trec doar puţin mai mult de 16 minute. De observat că 3,732 = 1/0,268, adică sunt numere inverse.

Căile luminii pentru imagini schimbate în timpul călătoriei
Stânga: De la Pământ la navă. Dreapta: De la navă la Pământ.
Liniile roşii indică imaginile de frecvenţă joasă primite
Liniile albastre indică imaginile de frecvenţă înaltă primite

Diagramele spaţiu-timp x − t din stânga arată calea semnalelor luminoase trimise între Pământ şi navă (diagrama 1) şi între navă şi Pământ (diagrama 2). Aceste semnale poartă imaginile fiecărui frate, cu ceasul corespunzător, către celălalt frate. Linia verticală neagră este calea Pământului prin spaţiu-timp iar celelalte muchii ale triunghiului arată calea navei prin spaţiu-timp (ca şi în diagrama Minkowski de mai sus). Prima diagramă arată semnalele care transportă imaginea de la Pământ la navă, iar cea de-a doua arată semnalele trimise de la navă spre Pământ. Din punctul de vedere al transmiţătorului, el transmite acestea la intervale egale (o dată pe oră) conform propriului său ceas; dar conform fratelui care recepţionează aceste semnale, ele nu sunt primite la intervale de timp egale, conform ceasului acestuia.

După ce nava a atins viteza sa de croazieră de 0,866 c, fiecare frate vede trecând 1 secundă în imaginea recepţionată de la celălalt frate la fiecare 3,73 secunde din timpul său. Adică fiecare vede imaginea ceasului celuilalt mergând mai încet, nu doar cu factorul ε ci şi mai încet, datorită efectului Doppler observaţional. Aceasta este arătată în figuri prin liniile roşii. La un anumit moment, imaginile recepţionate de fiecare frate se schimbă astfel încât acesta vede 3,73 secunde trecănd în imagine pentru fiecare secundă din timpul său. Adică, semnalele primite au crescut în frecvenţă datorită deplasării Doppler. Aceste imagini de înaltă frecvenţă sunt reprezentate în figură de liniile albastre.

Asimetria în imaginile deplasate Doppler

Asimetria dintre Pământ şi nava spaţială se manifestă în această diagramă prin faptul că imaginile mai deplasate spre albastru (mai rapide) sunt primite de navă şi cele mai deplasate spre roşu sunt primite de Pământ (mai lente) sunt recepţionate de Pământ. Cu alte cuvinte, nava spaţială vede imaginea schimbându-se de la o imagine deplasată spre roşu într-una deplasată spre albastru la punctul de întoarcere, la 2,57 de ani după plecare; Pământul vede imaginea navei schimbându-se de la una deplasată spre roşu într-una deplasată spre albastru după 9,59 ani (aproape de finalul perioadei când nava este absentă). Mai există însă o altă asimetrie a imaginilor: fratele de pe Pământ îl vede pe cel de pe navă îmbătrânind în acelaşi ritm în imaginile deplasate spre roşu şi în cele deplasate spre albastru; fratele din navă îl vede pe cel de pe Pământ îmbătrânind în ritmuri diferite în imaginile deplasate spre roşu şi în cele deplasate spre albastru.

Calculul duratelor de timp pe baza diagramelor Doppler

Fratele de pe navă vede imaginile de frecvenţă joasă (deplasate spre roşu) timp de 2,57 ani. De-a lungul acestei perioade, el vede fratele de pe Pământ în imagini cum a îmbătrânit cu 2,57/3,73 = 0,69 ani. Apoi el vede imagini de frecvenţă înaltă (deplasate spre albastru) de-a lungul celorlalţi 2,57 de ani ai drumului său. În acest timp, el îşi vede fratele de pe Pământ în imagini îmbătrânind cu 2,57×3,73 = 9,59 ani. La sfârşitul călătoriei, imaginea fratelui de pe Pământ a îmbătrânit cu 0,69 + 9,59 = 10,28 ani (deci fratele de pe Pământ este cu 10,28 de ani mai în vârstă).

Fratele de pe Pământ vede timp de 9,59 ani imagini deplasate spre roşu ale fratelui din navă, timp în care fratele de pe navă aparent îmbătrâneşte cu 9,58/3,73 = 2,57 ani. Apoi vede imagini rapide (deplasate spre albastru) timp de 0,69 ani până când nava soseşte înapoi. În imaginile rapide, fratele de pe navă înbătrâneşte cu 0,69×3,73 = 2,57 ani. Fratele de pe navă a îmbătrânit în total în imaginile care ajung pe Pământ cu 2,57+2,57 = 5,14 ani, deci fratele de pe navă se întoarce mai tânăr (pentru el au trecut 5,14 ani spre deosebire de 10,28 ani pe Pământ).

Distincţia între ce văd fraţii şi ce calculează

Pentru a evita confuzia, trebuie notată distincţia dintre ce vede fiecare frate şi ce ar calcula fiecare. Fiecare vede o imagine a fratelui său despre care ştie că a plecat la un moment de timp din trecut şi despre care ştie că este deplasată Doppler. Niciunul din ei nu consideră că vârsta fratelui său este cea aparentă din imagine. În plus, el nu confundă viteza cu care fratele din imagine îmbătrâneşte cu viteza cu care fratele din realitate îmbătrânea la momentul transmiterii imaginii.

• Dacă vrea să calculeze momentul când fratele său avea vârsta pe care o arată în imagine (adică cât de bătrân era el însuşi atunci), trebuie să determine cât de departe era de fratele său, la momentul emiterii semnalului — cu alte cuvinte, trebuie să considere simultaneitatea cu un eveniment îndepărtat.
• Dacă doreşte să calculeze cât de repede îmbătrânea fratele său când a fost transmisă imaginea, face ajustări după deplasarea Doppler. De exemplu, când primeşte imagini de înaltă frecvenţă (care îl arată pe frate său îmbătrânind rapid), cu frecvenţa , nu trage concluzia că fratele său îmbătrânea atât de rapid la momentul generării imaginii, cum nu ar trage nici concluzia asupra frecvenţei sirenei unei ambulanţe în mişcare. El ştie că efectul Doppler a mărit frecvenţa imaginii cu un factor de . Deci el calculează că fratele său îmbătrânea cu o viteză de

când a fost emisă imaginea. Un calcul similar arată că fratele său îmbătrânea cu aceeaşi viteză redusă de în toate imaginile de joasă frecvenţă.

Simultaneitatea în calculul deplasării Doppler

Poate fi dificil de văzut locul unde intervine simultaneitatea în calculul deplasării Doppler, şi într-adevăr calculele sunt adesea preferate deoarece în ele nu trebuie avut grijă de simultaneitate. După cum se vede mai sus, fratele de pe navă poate converti viteza recepţionată şi deplasată Doppler într-o viteză mai scăzută a ceasului celuilalt şi pentru imaginile deplasate spre roşu şi pentru cele deplasate spre albastru. Dacă ignoreă simultaneitatea ar putea spune că fratele său îmbătrâneşte cu viteză scăzută de-a lungul întregii călătorii şi deci că el ar trebui să fie mai tânăr. A ajuns exact de unde a plecat cu raţionamentul, şi trebuie să ţină cont de schimbarea în noţiunea de simultaneitate la momentul întoarcerii. Viteza pe care o poate calcula pentru imagine (cu efectul Doppler corectat) este viteza ceasului fratelui de pe Pământ la momentul transmiterii imaginii, nu la momentul recepţionării acesteia. De vreme ce recepţionează un număr inegal de imagini deplasate spre roşu şi de imagini deplasate spre albastru, ar trebui să îşi dea seama că emisiile deplasate spre roşu şi cele deplasate spre albastru nu au fost emise de-a lungul unor perioade de timp egale pentru fratele geamăn de pe Pământ, şi deci trebuie să ţină cont de simultaneitatea la distanţă.

Rezolvarea paradoxului în relativitatea generalizată

Problema soluţiei din relativitatea generalizată este cum percepe fratele călător situaţia din timpul accelerării pentru întoarcere. Această problemă este bine descrisă în cadrul soluţiei paradoxului gemenilor din 1918 oferită de Einstein^[2]. În această soluţie s-a observat că din punctul de vedere al călătorului, calculul fiecărui drum separat este echivalent cu cel din relativitatea restrânsă, în care ceasul de pe Pământ merge mai încet decât călătorul. De exemplu, dacă ceasurile de pe Pământ pierd 1 zi la fiecare drum, cantitatea cu care vor rămâne în urmă ceasurile de pe Pământ doar datorită vitezei va fi de 2 zile. Acum sistemul accelerat este privit ca fiind staţionar, iar descrierea fizică a ceea ce se întâmplă la punctul de întoarcere trebuie să producă un efect contrar egal cu dublul acelei cantităţi, şi anume avansul cu 4 zile al ceasurilor de pe Pământ. Atunci ceasul călătorului va ajunge să fie în urmă cu 2 zile faţă de ceasurile de pe Pământ, după cum stipulează relativitatea restrânsă.

Mecanismul care determină ceasul fratelui rămas acasă să o ia înainte este dilatarea temporală gravitaţională. Când un observator găseşte că obiectele în mişcare inerţială sunt accelerate în raport cu ele însele, acele obiecte sunt într-un câmp gravitaţional din punctul de vedere al relativităţii. Pentru fratele călător, la punctul de întoarcere, acest câmp gravitaţional umple universul. (Trebuie accentuată ideea că, conform explicaţiei lui Einstein, acest câmp gravitaţional este la fel de "real" ca orice alt câmp, dar în interpretarea modernă el este doar perceput deoarece este cauzat de accelerarea navei). Într-un câmp gravitaţional, ceasurile bat într-un ritm de t' = t(1 + Φ / c²) unde Φ este potenţialul gravitaţional. În acest caz, Φ = gh unde g este acceleraţia observatorului în deplasare în timpul întoarcerii, iar h este distanţa până la fratele rămas acasă. h este o valoare pozitivă în acest caz, fiindcă nava este accelerată către fratele rămas acasă, plasându-l astfel pe acesta la un potenţial gravitaţional mai mare. Datorită distanţei mari dintre fraţi, ceasul celui de pe Pământ va părea accelerat sufiecient de mult încât să explice diferenţa dintre timpii proprii observaţi de cei doi fraţi. Nu este o întâmplare că această accelerare este suficientă pentru a explica deplasarea de simultaneitate descrisă mai sus.

Deşi aceasta este considerată o soluţie ce ţine de "relativitatea generalizată", de fapt ea este elaborată pe baza unor date ce rezultă din teoria relativităţii restrânse pentru observatori acceleraţi pe care Einstein a descris-o încă din 1907 (anume principiul de echivalenţă şi dilatarea temporală gravitaţională). Se poate arăta că soluţia din relativitatea generalizată pentru un câmp gravitaţional static omogen şi soluţia din relativitatea restrânsă pentru acceleraţie finită produc rezultate identice.^[3]

Calculul rachetei accelerate

Fie ceasul K asociat cu "fratele rămas pe Pământ". Fie ceasul K' asociat cu nava. La evenimentul de plecare, ambele ceasuri sunt la 0.

Faza 1: Nava (cu ceasul K') pleacă cu acceleraţia proprie constantă a pentru un timp A măsurat de ceasul K până atinge o viteză v.

Faza 2: Nava merge cu viteza constantă v un timp T conform ceasului K.

Faza 3: Nava îşi declanşează motoarele în direcţia opusă lui K pentru un timp A conform ceasului K până când ajunge în repaus în raport cu K. Acceleraţia proprie constantă are valoarea −a, cu alte cuvinte, nava frânează.

Faza 4: Nava îşi păstrează motoarele active în direcţia opusă lui K, pe aceeaşi perioadă de timp A conform ceasului K, până K' ajunge la aceeaşi viteză v în raport cu K, dar acum în direcţia lui K (cu viteza −v).

Faza 5: Nava merge constant către K cu viteza v pe aceeaşi perioadă T conform ceasului K.

Faza 6: Nava îşi îndreaptă motoarele din nou către K, pentru a frâna cu o acceleraţie proprie constantă a pe o durată de timp A, tot conform ceasului K, până cele două ceasuri sunt aduse împreună.

Ştiind că ceasul K rămâne inerţial (în repaus), timpul propriu total acumulat Δt' al ceasului K' va fi dat de integrala

unde v(t) este viteza ceasului K' ca funcţie de t conform cu ceasul K.

Această integrală se poate calcula pe cele 6 faze:

Faza 1

Faza 2

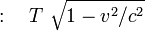
Faza 3

Faza 4

Faza 5

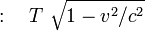
Faza 6

unde a este acceleraţia proprie, simţită de ceasul K' în timpul fazei de accelerare şi unde sunt valabile următoarele afirmaţii despre v, a şi A:

Deci ceasul de pe navă K' va prezenta o durat a timpului scurs de

ce poate fi reprezentată

pe când ceasul staţionar K arată un timp trecut de

adică pentru orice valoare posibilă pentru a, A, T şi v, mai mari decât citirea de pe ceasul K':

\Delta t'\," src="http://upload.wikimedia.org/math/f/7/2/f72044909be16be4eaafedaedf9d8297.png">

Note

1. ^ în Resnick şi Halliday, 1992
2. ^ Einstein, A. (1918) "Dialog über Einwände gegen die Relativitätstheorie", Die Naturwissenschaften 48, pp697-702, 29 noiembrie 1918 (în engleză: )
3. ^ Jones, Preston, Wanex, L.F. (Februarie 2006). "The clock paradox in a static homogeneous gravitational field". Foundations of Physics Letters 19 (1): 75–85.

Bibliografie

• Resnick, Robert şi Halliday, David (1992). Basic Concepts in Relativity. New York: Macmillan.

Evenimentele astronomice ale lunii septembrie

Zi Ora Eveniment

04	04:00	Saturn in conjunctie.
	20:30	Prima vizibilitate a Lunii in crestere.
07	16:05	Luna in primul patrar.
	17:00	Luna in apogeu, la o distanta de 404 214 km de Pamant.
11	07:00	Mercur in elongatie estica maxima (26°,9).
	23:00	Venus la 20' nord de Marte (nu este observabil in Europa).
13	04:00	Uranus in opozitie.
15	11:14	Luna plina.
20	05:00	Luna in perigeu, la o distanta de 368 886 km de Pamant.
22	07:05	Luna in ultimul patrar.
	17:44	Echinoxul (sau echinoctiul) de toamna. Inceputul toamnei in emisfera nordica si al primaverii in emisfera sudica. Ziua va fi egala cu noaptea.
28	06:10	Ultima vizibilitate a Lunii in descrestere.
	10:13	Luna noua.

Vizibilitatea lunii Dupa faza de Luna noua din 30 august, Luna in crestere va putea fi din nou observata din 4 septembrie, cand aceasta se va gasi, la crepusculul de seara, aproape de orizont. Pe 9 septembrie Luna poate fi gasita la 4° sub Jupiter, iar pe 27 septembrie aproape de Saturn. Luna in descrestere poate fi observata pentru ultima data pe 28 septembrie. Cele 4 faze ale Lunii vor avea loc dupa cum urmeaza: primul patrar - 7 septembrie, Luna plina - 15 septembrie, ultimul patrar - 22 septembrie, Luna noua - 28 septembrie.

Vizibilitatea planetelor

Mercur atinge pe 11 septembrie o elongatie estica maxima (26°,9), insa din pacate nici in aceasta luna nu poate fi observat. Venus se indeparteaza rapid de Soare, atingand catre sfarsitul lunii o distanta unghiulara de aproape 30°. De asemenea, nici Venus nu poate fi observata in aceasta luna. Marte nu este observabil in aceasta luna. Jupiter isi incheie pe 8 septembrie perioada de opozitie din acest an. Dupa ce s-a deplasat retrograd catre vest, din 9 mai, incepand din aceasta luna se va deplasa din nou catre est. Stralucirea aparenta a planetei va scade la -2.3° unitati. Saturn s-a aflat pe 4 septembrie in conjunctie cu Soarele, nefiind astfel vizibil in aceasta perioada. Incepand cu mijlocul lunii va putea fi observat din nou, pe cerul diminetii. Uranus se va afla pe 13 septembrie in opozitie cu Soarele, fiind astfel observabil in aceasta perioada in conditii optime. Planeta va putea fi gasita in constelatia Varsator. Neptun poate fi observat in constelatia Capricorn pana dupa miezul noptii.